Клод Шеннон: Математическая теория связи
<< Часть 1. Дискретные системы без шума | Оглавление | Часть 3. Математические основы >>

Часть 2. Дискретный зашумленный канал

Представление зашумленного дискретного канала

Рассмотрим теперь ситуацию, при которой сигнал подвергается воздействию шума либо в процессе передачи, либо на одном из концов канала. Это значит, что принятый сигнал не обязательно совпадает с тем, который был отправлен передатчиком. Можно выделить два различных класса таких ситуаций. Если один и тот же передаваемый сигнал всегда приводит к одинаковому сигналу в приемнике, то есть если принятый сигнал является однозначной функцией переданного, можно сказать, что имеет место искажение сигнала. Если эта функция имеет обратную, то есть каждый сигнал на в приемнике вызывается лишь одним сигналом в передатчике, это искажение может быть учтено, по крайней мере в принципе, применением соответствующей корректирующей операции к принятому сигналу.

Второй, более интересный класс, составляют ситуации, в которых передаваемый сигнал претерпевает не всегда одинаковые изменения. В таком случае мы можем считать принятый сигнал $E$ функцией как переданного $S$, так и шума $N$.

$$E = f(S,N)$$

Шум является случайной величиной, точно такой же, как и рассмотренное выше сообщение. В общем случае он может быть описан соответствующим стохастическим процессом. Наиболее общим случаем зашумленного канала, который мы рассмотрим, является обобщение описанного выше бесшумового канала с конечным числом состояний. Предположим, что есть конечное число состояний и набор вероятностей

$$p_{\alpha,i}(\beta,j).$$

Это вероятность того, что, если канал находится в состоянии $\alpha$ и передается символ $i$, на выходе будет принят символ $j$ и канал перейдет в состояние $\beta$. Здесь $\alpha$ и $\beta$ пробегают по всем возможным состояниям, $i$ - по всем возможным передаваемым символам, и $j$ - по всем возможным принимаемым. В случае независимого искажения последовательныхз символов состояние только одно, и канал описываетс набором вероятностей $p_i(j)$ принять символ $j$ при передаче $i$.

Если в канал подаются символы с источника, работают два случайных процесса: источник и шум. Соответственно, можно вычислить несколько различных энтропий. Это энтропия $H(x)$ источника (или энтропия на входе в канал, что эквивалентно предыдущему для несингулярного преобразователя), энтропия на выходе из канала, то есть принятого сигнала, которую мы будем обозначать $H(y)$. При отсуствии шума $H(y) = H(x)$. Совместную энтропию на входе и выходе обозначим $H(xy)$. Наконец, можно определить две условных энтропии $H_x(y)$ и $H_y(x)$, энтропии сигнала на выходе в случае, если известен сигнал на входе, и наоборот. Это величины связаны соотношением

$$H(x,y) = H(x) + H_x(y) = H(y) + H_y(x).$$

Каждую из этих энтропий можно определить в расчете как на одну секунду, так и на один символ.

Ошибочность и пропускная способность канала

Если канал является зашумленным, в общем случае невозможно с уверенностью восстановить исходное сообщение или переданный сигнал никаким преобразованием принятого сигнала $E$. Однако, существуют методы передачи информации, оптимальные для борььы с шумами. Рассмотрим эту задачу.

Пусть есть два возможных символа, 0 и 1, передаваемых с темпом 1000 символов в секунду с вероятностями $p_0 = p_1 = \frac12$. Таким образом, источник выдает информацию с темпом 1000 бит в секунду. При передаче наличие шума приводит к ошибкам, так что в среднем 1 из 100 символов принимается неправильно (0 вместо 1, или же 1 вместо 0). Каков темп передачи информации? Ясно, что он менбше 1000 бит в секунду, так как примерно $1\%$ символов принимается неправильно. Первым побуждением будет сказать, что темп передачи равен 990 бит в секунду (получено простым вычитанием количества неправильно принятых символов), однако этот ответ неудовлетворителен, так как не учитывает того факта, что приемник не знает, какие именно символы приняты неверно. Это становится очевидным из рассмотрения предельного случая, при котором принимаемый сигнал совершенно не зависит от передаваемого. В таком случае вероятность получить 1 равна $\frac12$, и примерно половина принятых символов случайно оказывается верной. По вышеприведенному определению оказывается, что темп передачи информации равен 500 бит в секунду, хотя очевидно, что информация не передается совсем. Настолько же ``хорошую'' передачу мы бы получили, совсем отключив канал и бросая монету в точке приема.

Очевидно, что корректной поправкой к количеству передаваемой информации будет количество информации, отсутствующее в принятом сигнале, или же неопределенность переданного сигнала при известном принятом. Вспоминая предшествующее обсуждение энтропии как меры неопределенности, разумно воспользоваться условной энтропией сообщения. Зная принятый сигнал, мы получаем меру этой утраченной информацией. Это действительно корректное определение, как будет показано далее. Таким образом, темп действительной передачи $R$ может быть получен вычитанием из темпа выдачи информации источником вреднего темпа условной энтропии.

$$R = H(x) - H_y(x)$$

Назовем для удобства условную энтропию $H_y(x)$ ошибочностью. Она характеризует среднюю неопределенность принятого сигнала.

В вышеприведенном примере, если принят ноль, апостериорная вероятность того, что был передан ноль, равна 0.99, тогда как того, что была передана единица - 0.01. Следовательно

или 81 бит в секунду. Можно сказать, что темп передачи информации равен $1000 - 81 = 919$. В предельном случае, когда переданный ноль с равной вероятностью принимается и как ноль, как единица, апостериорные вероятности равны $\frac12$, и

или 1000 бит в секунду. Темп передачи равен нулю, как и должно быть.

Нижеследующая теорема дает прямую наглядную интерпретацию ошибочностью, показывая, кроме того, что это единственная подходящая мера. Рассмотрим систему связи и наблюдателя (или вспомогательное устройство), способного видеть одновременно и передаваемую, и восстановленную по принимаемому сигналу информацию, содержащую ошибки из-за шума. Наблюдатель замечает эти ошибки и сообщает о них приемнику по ``корректирующему каналу'', позволяя их исправить. Ситуация схематически изображена на рисунке 8.


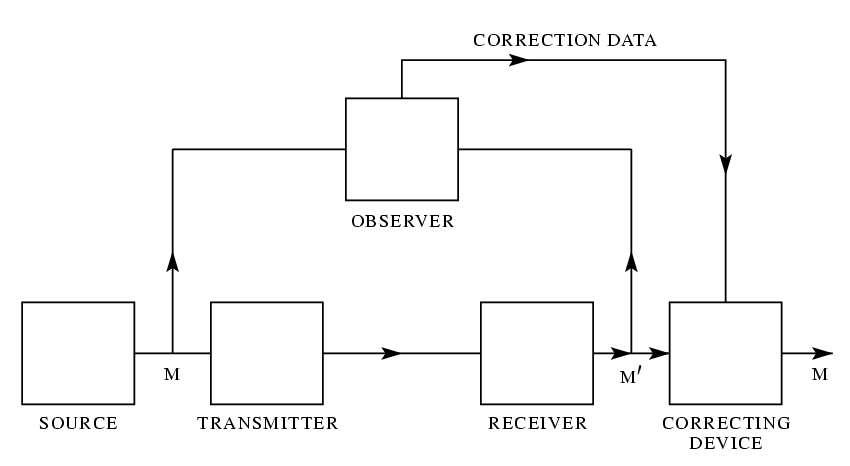
Рис.8. Схематическое изображение корректирующей системы.

Теорема 10: Если пропускная способность корректирующего канала $H_y(x)$, можно закодировать корректирующую информацию таким образом, что ее можно послать по этому каналу и скорректировать все ошибки за исключением их произвольно малой доли $\epsilon$. Это невозможно, если пропускная способность корректирующего канала меньше $H_y(x)$.

Грубо говоря, $H_y(x)$ - количество дополнительной информации, необходимой приемнику для коррекции принятого сообщения.

Для доказательства первой части рассмотрим длинные последовательности принятого сообщения $M'$ и исходного сообщения $M$. Есть логарифмически большое число $T H_y(x)$ сообщений $M$, которые могли бы привести к принятому сообщению $M'$. Таким образом, необходимо передавать $T H_y(x)$ двоичных цифр каждые $T$ секунд. Это может быть сделано при частоте ошибок $\epsilon$ в канале с пропускной способностью $H_y(x)$.

Второе утверждение может быть доказано, если Для доказательства второго утверждения заметим, что для любых дискретных случайных величин $x$, $y$, $z$

$$H_y(x,z) \ge H_y(x).$$

Левую часть можно преобразовать

$$H_y(z) + H_{yz}(x) \ge H_y(x) $$
$$H_{yz}(x) \ge H_y(x) - H_y(z) \ge H_y(x) - H(z).$$

Если мы отождествим $x$ с информацией, выдаваемой источником, $y$ - с принятым сигналом, и $z$ - сигналом, передаваемым по корректирующему каналу, то правая часть является разностью ошибочности и темпа передачи по корректирующему каналу. Если этот темп меньше ошибочности, то правая часть будет больше нуля, и $H_{yz}(x)>0$. А эта величина характеризует неопределенность сообщения при известных принятом и корректирующем сигналах. Когда она больше нуля, частота ошибок не может быть сделана произвольно малой.

Пример:

Рассмотрим случайные ошибки в последовательности двоичных цифр, с вероятностью $p$ того, что цифра неверна, и $q=1-p$ - что верна. Эти ошибки могут быть скорректированы, если известны их положения, потому корректирующий канал должен передавать лишь их положения. Это равносильно передаче двоичных знаков с вероятностями $p$ для 1 (неверная цифра), и $q$ - для 0 (верная цифра). Для этого требуется канал с пропускной способностью

$$- [p \log p + q \log q ]$$

что равно ошибочности исходной системы.

Темп передачи можно записать в двух других формах, используя вышеприведенные тождества. Имеем

Здесь первая запись уже была истолкована как разность посланного количества информации и ее неопределенности; вторая характеризует разность принятой информации и ее части, обусловленной шумом; третья же - разность суммы обеих информаций и совместной энтропии, то есть - число бит в секунду, общих для обеих. Таким образом, все эти выражения имеют определенное наглядное истолкование.

Пропускная способность зашумленного канала должна быть максимально возможным темпом передачи, то есть темпом, при котором источник соответствует каналу. Определим тогда пропускную способность как

$$C= \max \bigl(H(x) - H_y(x)\bigr)$$

где максимум вычисляется по отношению ко всем возможным источникам информации для канала. Для бесшумового канала $H_y(x) = 0$, и это определение сводится к данному ранее для такого канала, так как его энтропия равна его пропускной способности.

Основная теорема для дискретного канала с шумом

Может показаться удивительным то, что мы вводим определенную пропускную способность для зашумленного канала, тогда как надежная передача информации невозможна. Ясно, однако, что введением некоторой избыточности в передаваемую информацию вероятность ошибки может быть уменьшена. К примеру, при многократной передаче сообщения и последующем статистическом анализе принятой информации вероятность ошибки может быть сделана очень малой. Можно было бы, однако, решить, что для сведения этой вероятности к нулю избыточность информации должна возрастать бесконечно, что привело бы к падению темпа передачи до нуля. Однако это неверно. Если бы это было так, не могло бы быть однозначно определенной пропускной способности канала - была бы лишь пропускная способность при заданной частоте ошибок, или же при заданной ошибочности; эта пропускная способность стремилась бы к нулю при усилении ограничений на ошибки. На самом же деле определенная выше пропускная способность $C$ имеет вполне определенный смысл. Можно передать по каналу информацию с темпом $C$ с произвольно малой частотой ошибок или же ошибочностью путем соответствующего кодирования. При попытке же передачи с большим темпом $C+R_1$ неизбежно будет некоторая ошибочность, равная или большая $R_1$. Природа устроена так, что мы не сможем передать информацию с темпом, большим $C$.

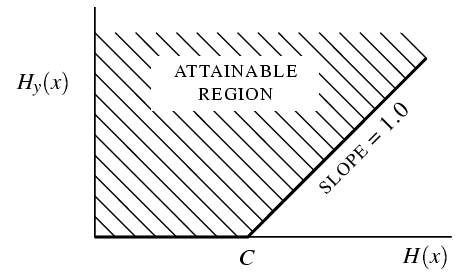
Данная ситуация иллюстрируется рис. 9. Темп поступления информации в канал отложен по горизонтальной оси, а ошибочность - по вертикальной. Все точки выше жирной линии в заштрихованной области достижимы, все точки ниже - недостижимы. Точки на линии в общем случае недостижимы, за исключением двух, которые обычно могут быть достигнуты.

Эти результаты являются оправданием вышеприведенного определения $C$, и сейчас мы их докажем.

Теорема 11: Пусть дискретный канал имеет пропускную способность $C$, а источник - энтропию в секунду $H$. При $H \le C$ существует такая система кодирования, что информация от источника может быть передана по каналу с произвольно малой вероятностью ошибки. При $H>C$ возможно так закодировать информацию, что ошибочность будет меньше $H-C+\epsilon$, где $\epsilon$ произвольно мало. Не существует способа кодирования, дающего ошибочность меньше $H-C$.

Способ доказательства первой части состоит не в явном построении требуемого способа кодирования, а в демонстрации того, что такой способ должен существовать в некотором множестве систем кодирования.


Рис.9.Допустимая ошибочность для заданной энтропии на входе в канал.

На самом деле мы проведем усреднение частоты ошибок по этому множеству и покажем, что это среднее может быть сделано меньшим $\epsilon$. Если среднее по некоторому набору чисел меньше $\epsilon$, должно быть хотя бы одно число из этого набора, меньшее $\epsilon$, что и послужит искомым доказательством.

Пропускная способность $C$ зашумленного канала была определена как

$$C= \max\bigl(H(x) - H_y(x)\bigr)$$

где $x$ - входная информация и $y$ - выходная. Максимизация проводится по всем возможным источникам информации для канала.

Пусть $S_0$ - источник, для которого достигается максимальная пропускная способность $C$. Если же этот темп не достигается ни одним источником, определим $S_0$ как источник, дающий максимальный темп передачи. Пусть этот источник подает информацию в канал. Рассмотрим возможные переданные и принятые последовательности достаточной длины $T$. Тогда справедливо следующее:

1. Передаваемые последовательности можно разделить на два класса - сообщения с высокой вероятностью, общим числом порядка $2^{T H(x)}$, и остальные с малой суммарной вероятностью.

2.Аналогично и принятые последовательности можно разделить на такие же классы.

3. Каждая высоковероятная принятая последовательность может вызываться примерно $2^{T H_y(x)}$ различными переданными. Вероятность того, что она вызывается остальными, мала.

Все $\epsilon$ и $\delta$ стремятся к нулю с ростом $T$ и приближением $S_0$ к источнику, максимизирующему темп передачи.

Эта ситуация изображена на рис. 10, где передаваемые последовательности представлены точками слева, а принятые - справа. Набор линий отражает множество возможных переданных последовательностей для данной принятой.


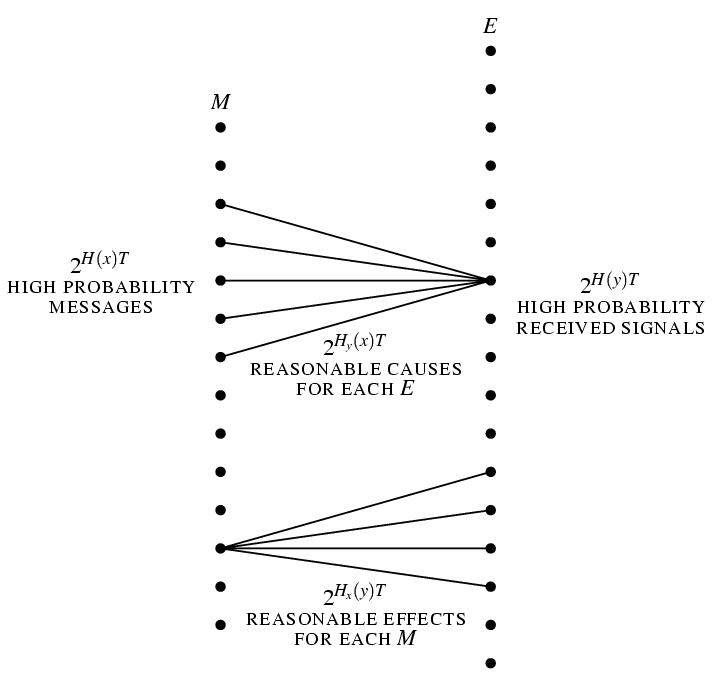
Рис.10. Схематическое изображение связи входной и выходной информации в канале.

Пусть теперь мы имеем источник с темпом $R$ таким, что

Обсуждение

Пример дискретного канала и его пропускная способность

Пропускная способность канала в некоторых специальных случаях

Пример эффективного кодирования

Приложение 1. Рост числа блоков символов при условии конечности числа состояний

Приложение 2. Получение выражения $H=-\sum p_i\log p_i$

Приложение 3. Теоремы об эргодичесих источниках

Приложение 4. Максимизация темпа для системы с ограничениями

<< Часть 1. Дискретные системы без шума | Оглавление | Часть 3. Математические основы >>
Астронет