Клод Шеннон: Математическая теория связи
<< Часть 2. Дискретный зашумленный канал | Оглавление | Часть 4. Непрерывный канал >>

Часть 3. Математические основы

В дальнейшем мы рассмотрим ситуации, в которых сигналы и/или сообщения являются непрерывными величинами, в противоположность рассмотренному ранее дискретному случаю. Непрерывный случай может быть получен предельным переходом из дискретного - делением непрерывного множества сообщений и сигналов на большое но конечное число малых областей и вычислением величин по такой дискретной системе. С уменьшением размеров отдельных областей эти параметры в общем случае стремятся к соответствующим величинам непрерывной задачи. Однако, появляются и некоторые новые эффекты, кроме того, акценты смещаются в направлении специализации общиз результатов для конкретных задач.

В непрерывном случае мы не будем пытаться получать результаты с как можно большей общностью или математической строгостью, так как это потребовало бы существенного углубления в абстрактную теорию меры и увело нас далеко от основной линии нашего исследования. Предварительное рассмотрение, однако, показывает, что теория может быть сформулирована полностью аксиоматически и строго так, что будет включать в себя как непрерывный, так и дискретный случаи, и многое другое. Определенноые вольности в предельных переходах в нашеи рассмотрении могут быть строго обоснованы для всех практически интересных ситуаций.

Множества и ансамбли функций

При рассмотрении непрерывного случая мы будем иметь дело с множествами и ансамблями функций. Множество функций, как следует из названия, есть просто набор или группа их, зависящих обычно от одной переменной, времени. Оно определяется явным заданием различных составляющих его функций, или же свойством, которым обладают это функции, а все остальные - нет. Приведем несколько примеров.

Назовем ансамблем функций множество их с мерой, посредством которой можно определить вероятность функции из этого множества, имеющей заданные свойства. (Математическим языком - функции принадлежат пространству с мерой, причем его полная мера равна единице.). К примеру, для множества

$$f_\theta(t)=\sin(t+\theta),$$

мы можем задать распределение вероятности для $\theta$, $P(\theta)$. Множество при этом становится ансамблем.

Приведем еше несколько примеров ансамблей.

Назовем ансамбль функций $f_\alpha(t)$ стационарным, если результаты расчета по нему не меняются при произвольном (фиксированном) сдвиге по времени. Ансамбль

$$f_\theta(t)=\sin(t+\theta)$$

стационарен, если $\theta$ распределена равномерно на интервале от $0$ до $2\pi$. При сдвиге каждой из функций на $t_1$ получаем

где $\varphi$ распределено равномерно от $0$ до $2\pi$. Каждая из фугкций меняется, но ансамбль как целое инвариантен по отношению к такому преобразованию. Остальные вышеприведенные примеры также являются стационарными.

Ансамбль является эргодическим, если от стационарен и в нем отсутствуют подмножества с вероятностью, отличной от 0 и 1, которые являются стационарными. Ансамбль

$$\sin(t+\theta)$$

является эргодическим. Ни одно из его подмножеств с вероятностью $\neq0,1$ не переходит в себя при произвольном сдвиге по времени. С другой стороны, ансамбль

$$a\sin(t+\theta)$$

с нормально распределенной $a$ и равномерно - $\theta$ стационарен, но не эргодичен, так как, к примеру, его подмножество с $a$ между 0 и 1 стационарно.

Среди вышеприведенных примеров третий и четвертый эргодичны, пятый, возможно, тоже. Если ансамбль эргодичен, можно (грубо) считать, что любая из его фкнкций является для него типичной. Более точно, известно, что для эргодического ансабмля среднее любой статистики по ансамблю равно (с вероятностью 1) среднему по времени для любой из функций (Это - заменитая эргодическая теорема (точнее, один из ее аспектов), доказанная в немного различных формулировках Бирковым, фон Нейманом и Купманом (Birkoff, von Neumann, Koopman), и обобщенная затем Винером, Хопфом, Гуревичем (Wiener, Hopf, Hurewicz) и другими. Литература по эргодической теории достаточно обширна, и мы отсылаем читателя к статьям этих авторов за точной и общей формулировкой; к примеру, см. E. Hopf, ``Ergodentheorie,'' Ergebnisse der Mathematik und ihrer Grenzgebiete, v. 5; ``On Causality Statistics and Probability,'' Journal of Mathematics and Physics, v. XIII, No. 1, 1934; N. Wiener, ``The Ergodic Theorem,'' Duke Mathematical Journal, v. 5, 1939.). Грубо говоря, можно считать, что каждая функция со временем проходит с соответствующей частотой все элементы формы всех остальных функций.

Точно так же, как мы производим некоторые операции над числами или функциями для получения новых чисел лил функций, мы можем производить некоторые операции над ансамблями для получения новых. Пусть, к примеру, у нас есть ансамбль функций $f_\alpha(t)$ и оператор $T$, переводящий каждую из функций $f_\alpha(t)$ в $g_\alpha(t)$

$$g_\alpha(t)=Tf_\alpha(t).$$

Меру вероятности для множества $g_\alpha(t)$ определим через меру для $f_\alpha(t)$. Вероятность некоторого подмножества $g_\alpha(t)$ равна вероятности его прообраза из $f_\alpha(t)$ (то есть такого подмножества, которое переводится действием оператора $T$ в данное). Физически это соответствует пропусканию ансамбля через некоторое устройство, к примеру - фильтр, выпрямитель или модулятор. Функции на выходе этого устройства образуют ансамбль $g_\alpha(t)$.

Устройство или оператор $T$ назовем инвариантным, если сдвиг входного сигнала соответствующим образом сдвигает выходной, то есть из

$$g_\alpha(t)=Tf_\alpha(t)$$

следует

$$g_\alpha(t+t_1)=Tf_\alpha(t+t_1)$$

для всех $f_\alpha(t)$ и $t_1$. Легко показать (см. приложение 5), что если оператор $T$ инвариантен и входной ансамбль стационарен, выходной ансамблю также будет стационарным. Аналогично, если входной ансамбль эргодичен, будет эргодичным и выходной.

Фильтр или выпрямитель инвариантны относительно любых преобразований времени, тогда как операция модуляции - нет, так как несущая частота имеет определенную временную структуру. Однако, модуляция инвариантна относительно всех преобразований, кратных периоду несущей частоты.

Винер (Wiener) обратил внимание на глубокую связь инвариантности физических устройств относительно временных сдвигов с теорией Фурье (Теория связи обязана Винеру основами свой философии и теории. Его классический доклад (NDRC report) The Interpolation, Extrapolation and Smoothing of Stationary Time Series (Wiley, 1949) содержит первую ясную и четкую формулировку теории связи как статистической задачи изучения операций над временными рядами. Эта работа, хотя и посвященная главным образом задачам линейного предсказания и фильтрации, является важным дополнением к данной статье. Хотелось бы также отметить его Cybernetics (Wiley, 1948), посвященную общей задаче связи и управления.). Так, он показал, что, если устройство является линейным и инвариантным, фурье-анализ дает подходящий математический аппарат для его описания.

Ансамбль функций является подходящим математическим представлением сообщений, выдаваемых непрерывным источником (к примеру, речи), сигналов, сформированных преобразователем, и возмущающего шума. Теория связи в корректной формулировке, как было отмечено Винером, должна иметь дело не с конкретными функциями, а с их ансамблями. Система связи должна разрабатываться не для конкретной речевой функции, и уж тем более не для синусоидального сигнала, а для ансамбля функций речи.

Ансамбли функций с ограниченным диапазоном частот

Если функция времени $f(t)$ ограничена интервалом частот от $0$ до $W$, то она полностью определяется набором своих значений в дискретном наборе точек с шагом $\frac1{2W}$ способом, представленным в нижеприведенной теореме (За доказательством и обсуждением отсылаем к работе автора ``Communication in the Presence of Noise'', опубликованной в Proceedings of the Institute of Radio Engineers, v. 37, No. 1, Jan., 1949, pp. 10--21.).

Теорема 13: Пусть $f(t)$ не содержит компонент с частотой, большей $W$. Тогда

$$f(t)=\sum_{-\infty}^\infty X_n\frac{\sin\pi(2Wt-n)}{\pi(2Wt-n)}$$

где

$$X_n=f\Bigl(\frac{n}{2W}\Bigr).$$

В этом разложении $f(t)$ представляется суммой ортогональных функций. Коэффициенты $X_n$ можно рассматривать как координаты в бесконечномерном ``пространстве функций'', в котором каждая функция соответствует только одной точке, и каждая точка - функции.

Функцию можно считать ограниченной временем $T$, если все ее значения $X_n$ за пределами этого интервала равны нулю. Таким образом, функции, ограниченные частотным диапазоном $W$ и временным - $T$, соответствуют точкам пространства размерности $2T W$.

Подмножество таких функций соответствует области в этом пространстве. К примеру, функции с полной энергией, меньшей $E$, соответствуют точкам внутри $2T W$-мерной сферы радиуса $r=\sqrt{2W E}$.

Ансамбль функций ограниченных длины и частотного диапазона можно представить распределением вероятности $p(x_1,\dots,x_n)$ в соответствующем $n$-мерном пространстве. Если же ансамбль не ограничен во времени, можно считать, что $2T W$ координат на интервале $T$ представляют часть функции, лежащую на этом интервале, а распределение вероятности $p(x_1,\dots,x_n)$ - статистическую структуру ансамбля интервалов такой длины.

Энтропия непрерывного распределения

Энтропия дискретного набора вероятностей $p_1,\dots,p_n$ была определена как

$$H=-\sum p_i\log p_i.$$

Определим аналогично и энтропию непрерывного распределения с плотностью $p(x)$

$$H=-\int_{-\infty}^\infty p(x)\log p(x)\,dx.$$

Для $n$-мерного распределения $p(x_1,\dots,x_n)$ имеем

При наличии двух аргументов $x$ и $y$ (которые, в свою очередь могут быть многомерными) совместная и условная энтропии имеют вид

и


где


Энтропии непрерывных распеределий сохраняют большинство (но не все) свойств дискретного случая. В частности,

Энтропия ансамбля функций

Рассмотрим эргодический ансамбль функций, ограниченных полосой частот ширины $W$. Пусть

$$p(x_1,\dots, x_n)$$

плотность функции распределения амплитуд $x_1,\dots,x_n$ в $n$ последовательных точках. Определим энтропию ансамбля в расчете на степень свободы как

$$H'=-\lim_{n\to\infty}\frac1n\int\dots\int p(x_1,\dots, x_n)\log p(x_1,\dots, x_n)\,dx_1\dots dx_n.$$

Можно также определить энтропию в секунду, поделив не на $n$, а на время $T$ в $n$ выборках. Так как $n=2T W$, $H=2W H'$.

При белом тепловом шуме $p$ гауссово, и

Для данной средней мощности $N$ белый шум обладает наибольшей возможной энтропией, что следует из свойств максимизации гауссова распределения, отмеченных выше.

Энтропия непрерывного стохастического процесса обладает многими свойствами, аналогичными дискретному случаю. В дискретном случае энтропия была связана с логарифмом вероятности длинных последовательностей и числом достаточно вероятных последовательностей большой длины. В непрерывном же случае она связана похожим образом с логарифмом плотности вероятности длинных выборок и обьемом достаточно большой вероятности в пространстве функций.

Более точно, если $p(x_1,\dots,x_n)$ непрерывно по всем $x_i$ для всех $n$, то для достаточно больших $n$

$$\Bigl|\frac{\log p}{n}-H'\Bigr|<\epsilon$$

для всех $(x_1,\dots,x_n)$ за исключением множества полной вероятности меньше $\delta$, где $\delta$ и $\epsilon$ произвольно малы. Это следует из свойства эргодичности при делении пространства на большое число маленьких ячеек.

Связь $H$ с обьемом можно установить следующим образом. При тех же условиях рассмотрим $n$-мерное пространство, соответствующее $p(x_1,\dots,x_n)$. Пусть $V_n(q)$ - наименьший обьем в этом пространстве, содержащий в себе полную вероятность $q$. Тогда

$$\lim_{n\to\infty}\frac{\log V_n(q)}{n}=H'$$

при $q$ не равно 0 или 1.

Это показывает, что для больших $n$ есть хорошо определенный обьем (как минимум в логарифмическом смысле) большой вероятности, и внутри него плотность вероятности достаточно донородна (опять же в логарифмическом смысле).

В случае белого шума фкнкция распределения дается выражением

$$p(x_1,\dots,x_n)=\frac{1}{(2\pi N)^{n/2}}\exp -\frac{1}{2N}\sum x_i^2.$$

Так как это зависит лишь от $\sum x_i^2$, поверхности равной плотности вероятности являются сферами и все распределение сферически-симметрично. Область большой вероятности является шаром радиуса $\sqrt{n N}$. При $n\to\infty$ вероятность находиться вне этой области радиуса $\sqrt{n(N+\epsilon)}$ стремится к нулю, и умноженный на $\frac1n$ логарифм ее обьема стремится к $\log\sqrt{2\pi e N}$.

В непрерывном случае удобно работать не с энтропией $H$ ансамбля, а с некоторой производной от нее величиной, которую мы будем называть мощностью энтропии. Определим ее как мощность ограниченного тем же диапазоном частот белого шума той же энтропии. Иными словами, если энтропия ансамбля равна $H$, то ее мощность есть

$$N_1=\frac{1}{2\pi e}\exp 2H'.$$

В геометрическом подходе это соответствует измерению обьема высокой вероятности квадратом радиуса шара того же обьема. Так как белый шум имеет наибольшую энтропию, мощность энтропии любого шума не превосходит его действительную мощность.

Таблица 1.
УсилениеФактор мощности энтропииУсиление мощности энтропии в децибелахИмпульсный отклик
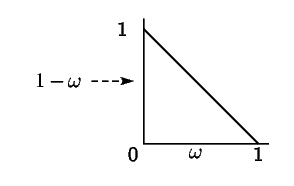$\frac{1}{e^2}$$-8.69$2}$
$\Bigl(\frac{2}{e}\Bigr)^4$$-5.33$$2\left[\frac{\sin t}{t^3}-\frac{\cos t}{t^2}\right]$
$0.411$$-3.87$$6\left[\frac{\cos t-1}{t^4}-\frac{\cos t}{2t^2}+\frac{\sin t}{t^3}\right]$
$\Bigl(\frac{2}{e}\Bigr)^2$$-2.67$$\frac{\pi}{2}\frac{J_1(t)}{t}$
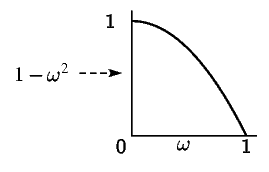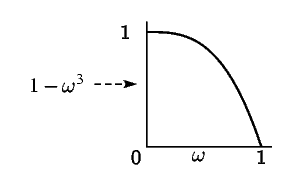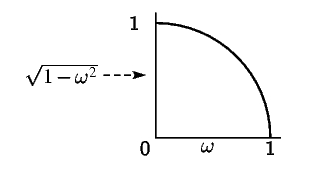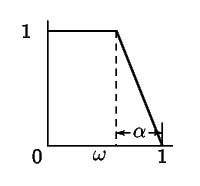$\frac{1}{e^{2\alpha}}$$-8.69\alpha$$\frac{1}{\alpha t^2}\bigl[\cos(1-\alpha)t-\cos t\bigr]$

Потери энтропии в линейных фильтрах

Теорема 14: При пропускании ансамбля с энтропией $H_1$ в расчете на степень свободы в полосе частот $W$ через фильтр с характеристической функцией $Y(f)$ энтропия выходного ансамбля равна

$$H_2=H_1+\frac1W\int_W \log|Y(f)|^2\,df.$$

Действие фильтра сводится к линейному преобразованию координат. Если мы рассмотрим различные частотные компоненты как исходную систему координат, новые частотные компоненты получаются из них умножением на некоторые факторы. Матрица преобразования координат, следовательно, диагонализуется в терминах этих координат. Якобиан преобразования тогда (для $n$ синусоидальных и

Энтропия суммы двух ансамблей

$n$ косинусоидальных компонент) имеет вид $$J=\prod_{i=1}^n|Y(f_i)|^2$$

где $f_i$ находятся на равных друг от друга расстояниях в полосе частот $W$. Это имеет место в пределе

$$\exp\frac1W\int_W\log|Y(f)|^2\,df.$$

Так как $J$ - константа, ее среднее значение равно самой величине, и, используя теорему об изменении энтропии при преобразовании координат, получаем искомое доказательство. Таким образом, если энтропия первого ансамбля равна $N_1$, то второго -

$$N_1\exp\frac1W\int_W\log|Y(f)|^2\,df.$$

Конечная мощность энтропии равна исходной, помноженной на геометрическое среднее усиления фильтра. Если усиление измеряется в децибелах (db), то мощность энтропии на выходе окажется больше входной на арифметическое среднее усиления на $W$.

В таблице 1 приведены потери мощности энтропии (и переведены в децибелы) для некоторых идеальных характеристик усиления. Кроме того, представлены импульсные отклики этих фильтров для $W=2\pi$ в предположении, что фаза равна нулю.

Потери энтропии для многих иных случаев могут быть получены из вышеприведенных. К примеру, фактор мощности энтропии $1/e^2$ применим также к любым характеристикам усиления, полученным из $1-\omega$ произвольным сохраняющим меру преобразованием оси $\omega$. К примеру, линейно возрастающее усиление $G(\omega)=\omega$ (или ``пилообразный зубец'') на интервале от 0 до 1 ведет к тем же самым потерям энтропии. Обратное усиление приводит к обращению фактора, следовательно, для $1/\omega$ фактор равен $e^2$. Возведение усиления в любую степень приводит к возведению в ту же степень фактора.

Если у нас есть два ансамбля функций $f_\alpha(t)$ и $g_\beta(t)$, мы можем образовать новый, ``сложив'' их. Пусть первый ансамбль имеет плотность вероятности $p(x_1,\dots,x_n)$, а второй - $q(x_1,\dots,x_n)$. Тогда плотность вероятности их суммы дается выражением

Физически это соответствует сложению сигналов или шумов, описываемых исходными ансамблями.

Следующий результат получается в приложении 6.

Теорема 15: Пусть средние мощности двух ансамблей суть $N_1$ и $N_2$, а мощности энтропии - $\overline N_1$ и $\overline N_2$. Тогда мощность энтропии их суммы, $\overline N_3$, ограничена

$$\overline N_1+\overline N_2\leq\overline N_3\leq N_1+N_2.$$

Гауссовский белый шум имеет отличительное свойство, состоящее в том, что он может поглотить любой другой сигнал или шум при его добавлении, и результирующая мощность энтропии будет примерно равна сумме мощностей белого шума и сигнала (измеряя от средней величины сигнала, равной обычно нулю), если сигнал достаточно мал по сравнению с шумом.

Рассмотрим $n$-мерное пространство функций, соответствующих этим ансамблям. Белый шум соответствует сферическому гауссовому распределению в этом пространстве, сигнал - некоторому другому, не обязательно гауссовому или сферически-симметричному. Пусть вторые моменты этого распределения относительно центра тяжести суть $a_{ij}$, то есть, для плотности вероятности $p(x_1,\dots,x_n)$,

где $\alpha_i$ - координаты центра тяжести. Теперь $a_{ij}$ - положительно определенная квадратичная форма, и мы может повернуть систему координат так, чтобы ее оси совпадали с осями этой формы. $a_{ij}$ тогда сводится к диагональному виду $b_{ii}$.Потребуем, чтобы все $b_{ii}$ были малы по сравнению с $N$, квадратом радиуса сферически-симметричного распределения.

В этом случае свертка сигнала с шумом дает примерно гауссовское распределение, которому соответствует квадратичная форма

$$N+b_{ii}.$$

Мощность энтропии такого распределения имеет вид

$$\Bigl[\prod(N+b_{ii})\Bigr]^{1/n}$$

или, приближенно,

$$=\Bigl[(N)^n+\sum b_{ii}(N)^{n-1}\Bigr]^{1/n}\doteq N+\frac1n\sum b_{ii}.$$

Последний член соответствует мощности сигнала, тогда как первый - мощности шума.

<< Часть 2. Дискретный зашумленный канал | Оглавление | Часть 4. Непрерывный канал >>
Астронет