Телетайп и телеграф - два простых примера дискретных каналов для передачи информации.
В общем случае будем называть дискретным каналом систему, посредством которой
последовательность выборов из набора элементарных символов ![]() может быть передана из одной точки в другую. Каждый из этих символов
может быть передана из одной точки в другую. Каждый из этих символов ![]() предполагается имеющим некоторую протяженность во времени
предполагается имеющим некоторую протяженность во времени ![]() (не обязательно одинаковую для различных символов). Не требуется возможность
передачи произвольной последовательности символов, вполне допустим вариант
с ограниченным набором разрешенных последовательностей. Это - возможные сигналы
в канале. К примеру, в телеграфии такими символами являются: (1)
точка, соответствующая замыканию линии на единичное время и размыканию той же
длительности, (2) тире, соответствующее замыканию линии на три единицы времени
и размыканию на одну, (3) промежуток между буквами, соответствующий,
к примеру, размыканию линии на три единицы времени, и (4) промежуток
между словами, соответствующий размыканию линии на шесть единиц времени.
Мы можем ограничить возможные последовательности символов, запретив к примеру
последовательные промежутки (так как два следующих друг за другом буквенных
промежутка идентичны промежутку между словами). Вопрос, который мы сейчас
рассмотрим, состоит в том, как определить пропускную способность такого канала.
(не обязательно одинаковую для различных символов). Не требуется возможность
передачи произвольной последовательности символов, вполне допустим вариант
с ограниченным набором разрешенных последовательностей. Это - возможные сигналы
в канале. К примеру, в телеграфии такими символами являются: (1)
точка, соответствующая замыканию линии на единичное время и размыканию той же
длительности, (2) тире, соответствующее замыканию линии на три единицы времени
и размыканию на одну, (3) промежуток между буквами, соответствующий,
к примеру, размыканию линии на три единицы времени, и (4) промежуток
между словами, соответствующий размыканию линии на шесть единиц времени.
Мы можем ограничить возможные последовательности символов, запретив к примеру
последовательные промежутки (так как два следующих друг за другом буквенных
промежутка идентичны промежутку между словами). Вопрос, который мы сейчас
рассмотрим, состоит в том, как определить пропускную способность такого канала.
В случае телетайпа, в котором все символы имеют одну и ту же длительность и
разрешена любая комбинация 32-х символов, ответ прост. Каждый символ представляет собой
пять бит информации. Если система связи передает ![]() символов в секунду,
естественно сказать, что пропускная способность канала
символов в секунду,
естественно сказать, что пропускная способность канала ![]() бит
в секунду. Это не значит, что телетайп всегда передает информацию с
такой скоростью - это лишь максимально возможный темп, и будет или нет он достигаться -
зависит от источника информации, подаваемой в канал (см. далее)
бит
в секунду. Это не значит, что телетайп всегда передает информацию с
такой скоростью - это лишь максимально возможный темп, и будет или нет он достигаться -
зависит от источника информации, подаваемой в канал (см. далее)
Для более общего случая различной длины символов и ограничений на разрешенные последовательности дадим следующее определение:
Определение: Пропускная способность ![]() канала дается
выражением
канала дается
выражением
где ![]() - число возможных сигналов длительности
- число возможных сигналов длительности ![]() .
.
Легко видеть, что в случае телетайпа этот результат сводится в предыдущему.
Можно показать, что этот предел в большинстве интересующих нас случаев существует
и является конечным. Предположим, что разрешены все последовательности символов
![]() длительностью
длительностью ![]() соответственно.
Какова пропускная способность канала? Если
соответственно.
Какова пропускная способность канала? Если ![]() - число последовательностей
длительности
- число последовательностей
длительности ![]() ,
,
Полное число равно сумме чисел последовательностей, оканчивающихся на
![]() , то есть
, то есть ![]() ,
соответственно. Согласно широко известному результату дискретного анализа,
,
соответственно. Согласно широко известному результату дискретного анализа,
![]() при больших
при больших ![]() асимптотически стремится к
асимптотически стремится к
![]() , где
, где ![]() - наибольший действительный корень
характеристического уравнения:
- наибольший действительный корень
характеристического уравнения:
и следовательно
При наличии ограничений на разрешенные последовательности символов мы зачастую
также можем получить разностное уравнение такого типа и найти ![]() из
характеристического уравнения. В вышеупомянутом случае телеграфной системы
из
характеристического уравнения. В вышеупомянутом случае телеграфной системы
что получается при учете последнего и предпоследнего символов.
Следовательно, ![]() равно
равно ![]() , где
, где
![]() - положительный корень уравнения
- положительный корень уравнения
![]() .
Решая его, находим
.
Решая его, находим ![]() .
.
Достаточно общим видом ограничений на возможные последовательности символов
может быть следующий. Рассмотрим множество возможных состояний ![]() .
В каждом состоянии могут передаваться лишь некоторые символы из набора
.
В каждом состоянии могут передаваться лишь некоторые символы из набора
![]() (различные подмножества в различных состояниях).
При передаче одного из этих символов состояние изменяется в зависимости как
от предыдущего состояния, так и от переданного символа. Простым примером такой
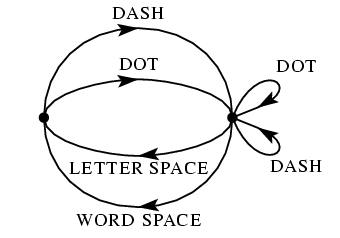
системы является телеграф, который может находиться в одном из двух состояний
в зависимости от того, был ли последним переданным символом 'пробел'. Если
да, то может быть посланы только точка или тире, и состояние изменится на
противоположное. Если же нет, может быть послан произвольный символ, и состояние
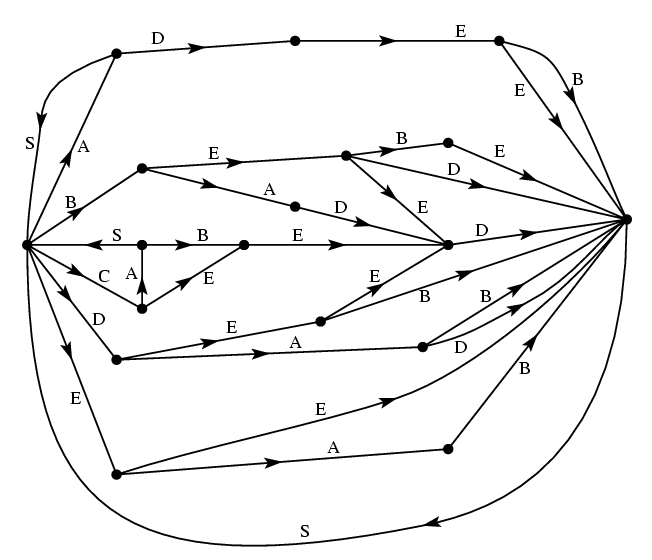
изменится, если посланный символ - 'пробел'. Эта ситуация иллюстрируется
линейным графом, изображенным на рис.2.
(различные подмножества в различных состояниях).
При передаче одного из этих символов состояние изменяется в зависимости как
от предыдущего состояния, так и от переданного символа. Простым примером такой
системы является телеграф, который может находиться в одном из двух состояний
в зависимости от того, был ли последним переданным символом 'пробел'. Если
да, то может быть посланы только точка или тире, и состояние изменится на
противоположное. Если же нет, может быть послан произвольный символ, и состояние
изменится, если посланный символ - 'пробел'. Эта ситуация иллюстрируется
линейным графом, изображенным на рис.2.
Теорема 1. Пусть ![]() - длительность символа
- длительность символа
![]() , разрешенного в состоянии
, разрешенного в состоянии ![]() и приводящего к переходу
системы в состояние
и приводящего к переходу
системы в состояние ![]() . Тогда пропускная способность канала
. Тогда пропускная способность канала ![]() равняется
равняется ![]() , где
, где ![]() - наибольший действительный
корень детерминистического уравнения
- наибольший действительный
корень детерминистического уравнения
где ![]() при
при ![]() и равно нулю иначе.
и равно нулю иначе.
К примеру, в случае телеграфа (рис. 2) детерминант равен
что при раскрытии дает вышеприведенное уравнение для данного случая.
Мы видели, что при достаточно общих условиях логарифм числа возможных сигналов в дискретном канале линейно растет со временем. Пропускная способность канала может быть охарактеризована темпом этого роста, числом бит в секунду, необходимых для передачи данного конкретного сигнала.
Рассмотрим теперь источник информации. Как он может быть описан математически, и сколько бит информации в секунду он производит? Важным тут является знание о статистике этого источника, что позволяет понизить требуемую пропускную способность канала выбором соответствующей кодировки - представления информации. В телеграфии, к примеру, передаваемые сообщения состоят из последовательностей букв. Эти последовательности, однако, не являются совершенно случайными. В общем слуяае они образуют предложения и имеют статистическую природу, скажем, английского языка. Буква E встречается чаще Q, последовательность TH - чаще, чем XP. Наличие такой структуры позволяет получить выигрыш во времени передачи сообщения (или пропускной способности канала), соответствующим образом его кодируя. Именно такой подход используется в телеграфии, где самый короткий символ - точка - исплльзуется для наиболее часто используемой английской буквы E, в то время как самые редкие - Q, X, Z - представляются более длинными последовательностями точек и тире. Еще больший выигрыш во времени передачи достигается в некоторых коммерческих системах кодирования, в которых наиболее распространенные фразы и выражения заменяются четырех- или пятибуквенными комбинациями. Использующиеся в настоящее время стандартизованные поздравительные и приветственные телеграммы также позволяют кодировать церые предложения достаточно короткими последовательностями чисел. в настоящее время
Можно считать, что дискретный источник формирует сообщение символ за символом, выбирая их в соответствии с некоторой вероятностью, зависящей как от номера символа, так и от предыдущих выборов. Физическая система, или же математическая модель системы, генерирующей такую последовательность символов в соответствии с набором вероятностей, представляет собой стохастический процесс (См., например, S. Chandrasekhar, ``Stochastic Problems in Physics and Astronomy,'' Reviews of Modern Physics, v. 15, No. 1, January 1943, p. 1.). Таким образом, мы можем рассматривать дискретный источник как стохастический процесс, и наоборот, любой стохастический процесс, генерирующий дискретную последовательность символов из ограниченного множества можно считать дискретным источником. Это включает в себя:
B D C B C E C C C A D C B D D A A E C E E A A B B D A E E C A C E E B A E E C B C E A D.Данная последовательность была построена с использованием таблицы случайных чисел(Kendall and Smith, Tables of Random Sampling Numbers, Cambridge, 1939.).
A A A C D C B D C E A A D A D A C E D A E A D C A B E D A D D C E C A A A A A D.
(C)
Более сложная структура может быть получена при отказе от взаимной
независимости отдельных процедур выбора - то есть тогда, когда каждый
последующий символ зависит от предыдущих. В простейшем случае каждый символ
зависит лишь от предыдущего и не зависит от более ранних. Статистическая
структура тогда может быть представлена набором вероятностей перехода
![]() , то есть вероятностей того, что за символом
, то есть вероятностей того, что за символом ![]() будет следовать символ
будет следовать символ ![]() . Вторым равноценным методом описания
такой структуры являются вероятности 'диграмм' (двухбуквенных комбинаций
. Вторым равноценным методом описания
такой структуры являются вероятности 'диграмм' (двухбуквенных комбинаций ![]() )
)
![]() . Частоты встречаемости букв
. Частоты встречаемости букв ![]() (вероятность
буквы
(вероятность
буквы ![]() ), вероятности перехода
), вероятности перехода ![]() и вероятности
диграмм
и вероятности
диграмм ![]() связаны следующими выражениями:
связаны следующими выражениями:
Для примера возьмем три буквы A, B,C с таблицами вероятностей:
A B B A B A B A B A B A B A B B B A B B B B B A B A B A B A B A B B B A C A C A B B A B B B B A B B A B A C B B B A B A.Следующим по сложности будет учет частот встречаемости триграмм, то есть ситуация, при которой выбор текущего символа зависит лишь от двух предшествующих. В данной ситуации требуется знание вероятностей триграмм
| .10 | A | .16 | BEBE | .11 | CABED | .04 | DEB |
| .04 | ADEB | .04 | BED | .05 | CEED | .15 | DEED |
| .05 | ADEE | .02 | BEED | .08 | DAB | .01 | EAB |
| .01 | BADD | .05 | CA | .04 | DAD | .05 | EE |
DAB EE A BEBE DEED DEB ADEE ADEE EE DEB BEBE BEBE BEBE ADEE BED DEED DEED CEED ADEE A DEED DEED BEBE CABED BEBE BED DAB DEED ADEB.Если все слова имеют ограниченную длину, данный процесс сводится к одному из вышеописанных, однако описание его будет проще в терминах структуры и вероятностей слов. Можно пойти далее и ввести вероятности перехода между словами, и так далее.
Такие искусственные языки полезны для формулировки простых задач и примеров
различных возможностей. Мы можем также приближенно описать некоторый
естественный язык серией простых искусственных. Нулевым приближением такого рода
будет модель с равновероятными независимыми буквами, следующим шагом может
служить учет различных вероятностей букв в естественном языке
(Вероятности букв, диграмм и триграмм даются в
Secret and Urgent by Fletcher Pratt, Blue Ribbon Books, 1939.
Частоты встречаемости отдельных слов приведены в Relative Frequency of English
Speech Sounds, G. Dewey, Harvard University Press, 1923.).
Так, в первом приближении для английского языка буква E будет выбираться
с вероятностью 0.12, а W - 0.02, но не будет никакого влияния букв друг
на друга, и не будет заметна тенденция к образованию наиболее частых буквосочетаний,
таких как TH или ED. Во втором приближении необходимо учесть
структуру диграмм - после выбора одной из букв следующая выбирается уже согласно
соответствующей условной вероятности, что требует знания частоты диграмм ![]() .
На следующем шаге вводится структура триграмм - каждая буква зависит уже
от двух предшествующих.
.
На следующем шаге вводится структура триграмм - каждая буква зависит уже
от двух предшествующих.
Для иллюстрации того, как эта серия приближений описывает естественный язык, были построены типичные последовательности приближений для английского языка. Во всех случаях использовался 27-символьный ``алфавит'' - 26 букв и пробел.
XFOML RXKHRJFFJUJ ZLPWCFWKCYJ FFJEYVKCQSGHYD QPAAMKBZAACIBZLHJQD.
OCRO HLI RGWR NMIELWIS EU LL NBNESEBYA TH EEI ALHENHTTPA OOBTTVA NAH BRL.
ON IE ANTSOUTINYS ARE T INCTORE ST BE S DEAMY ACHIN D ILONASIVE TUCOOWE AT TEASONARE FUSO TIZIN ANDY TOBE SEACE CTISBE.
IN NO IST LAT WHEY CRATICT FROURE BIRS GROCID PONDENOME OF DEMONSTURES OF THE REPTAGIN IS REGOACTIONA OF CRE.
REPRESENTING AND SPEEDILY IS AN GOOD APT OR COME CAN DIFFERENT NATURAL HERE HE THE A IN CAME THE TO OF TO EXPERT GRAY COME TO FURNISHES THE LINE MESSAGE HAD BE THESE.
THE HEAD AND IN FRONTAL ATTACK ON AN ENGLISH WRITER THAT THE CHARACTER OF THIS POINT IS THEREFORE ANOTHER METHOD FOR THE LETTERS THAT THE TIME OF WHO EVER TOLD THE PROBLEM FOR AN UNEXPECTED.
С каждым шагом заметно возрастает сходство с английским языком. Заметим, что приведенные примеры сохраняют достаточно похожую на оригинал структуру и далеко за рамками соответствующего приближения. Так, второе приближение дает приемлемый текст на уровне двухбуквенных сочетаний, но четырехбуквенные комбинации в нем также являются достаточно схожими с английским языком; фигурирующие в последнем примере комбинации четырех и более слов также вполне могут встречаться в реальных предложениях. Так, фраза из 10 слов ``attack on an English writer that the character of this'' не является совсем уж бессмысленной. Видно, что достаточно сложный стохастический процесс может являться вполне удовлетворительной моделью дискретного источника.
Два первых примера построены с использованием книги случайных чисел и таблицы частот букв. Похожий метод можно было бы использовать и для последующих, так как частоты диграмм и триграмм известны, однако мы воспользовались иным, более простым подходом. Для построения второго приближения, например, открывалась случайным образом книга и выбиралась случайная буква, которая записывалась; затем книга открывалась на другой странице и искалась первая двухбуквенная комбинация, начинающаяся с уже отобранной буквы, и записывалась следующая буква. Затем процедура повторялась. Похожий подход использовался и для остальных примеров. Было бы интересным построить также и следующие приближения, однако это требует слишком больших затрат времени и сил.
Стохастические процессы описанного выше типа в математике известны как
марковские процессы и достаточно широко освещены в литературе
(за подробным изложением отсылаем читателя к книге M. Frechet,
Methode des fonctions arbitraires. Theorie des evenements
en chane dans le cas d'un nombre fini d'etats possibles, Paris,
Gauthier-Villars, 1938.). В общем случае их можно описать следующим
образом. Существует конечное число возможных состояний системы ![]() ,
кроме того, известен набор вероятностей перехода
,
кроме того, известен набор вероятностей перехода ![]() системы
из состояния
системы
из состояния ![]() в состояние
в состояние ![]() . Чтобы сделать
такой марковский процесс источником информации, достаточно предположить, что
он выдает по одной букве в момент каждого перехода. Различные состояния системы
в таком случае соответствуют ``остаточному влиянию'' предшествующих букв.
. Чтобы сделать
такой марковский процесс источником информации, достаточно предположить, что
он выдает по одной букве в момент каждого перехода. Различные состояния системы
в таком случае соответствуют ``остаточному влиянию'' предшествующих букв.
Эту ситуацию можно представить в виде графов, как показано на рис.3, 4 и 5.
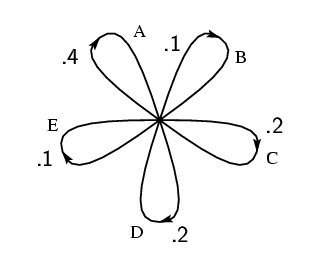
Состояния здесь представлены вершинами графа, а вероятности и соответствующие им буквы приведены рядом с соответствующими линиями переходов. Рис. 3 соответствует примеру (B) главы 2, а рис. 4 - примеру (C)
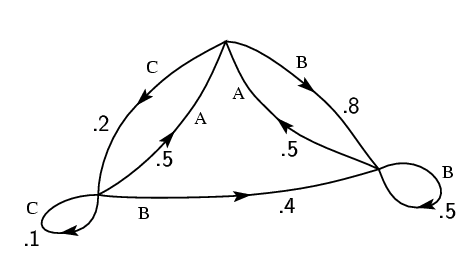
У системы, изображенной на рис. 3, есть лишь одно состояние, так как выбираемые
буквы независимы. На рис. 4 число состояний равно числу букв; в случае
учета триграммной структуры их число равно ![]() , что соответствует
возможным парам предшествующих букв. На рис. 5 изображен граф, соответствующий
структуре слов из примера (D) (S обозначает символ пробела).
, что соответствует
возможным парам предшествующих букв. На рис. 5 изображен граф, соответствующий
структуре слов из примера (D) (S обозначает символ пробела).
Как уже было отмечено, дискретный источник в наших задачах может рассматриваться как марковский процесс. Среди всех возможных марковских процессов можно выделить группу со свойствами, важными для теории связи. В этот класс входят так называемые ``эргодические'' процессы, и мы будем называть соответствующие источники эргодическими. Хотя строгое определение эргодического процесса достаточно запутанно, основная идея проста. Для эргодического процесса все сгенерированные последовательности обладают одинаковыми статистическими свойствами, то есть, к примеру, частоты встречаемости букв, диграмм и тек далее, оцененные по отдельным последовательностям, сходятся с ростом длины выборок к определенным пределам, не зависящим от последовательности. На самом деле это верно не для всякой последовательности, однако множество последовательностей, для которых это не выполняется, имеет меру ноль (то есть обладает нулевой вероятностью). Грубо свойство эргодичности означает статистическую однородность.
Все вышеприведенные примеры искусственных языков являются эргодическими. Это связано со структурой соответствующих графов. Если граф обладает двумя следующими свойствами, соответствующий процесс будет эргодическим:
Если выполняется только первое из условий, а второе нарушено, т.е. наибольший
общий делитель равен ![]() , последовательность имеет некоторую
периодическую структуру. Различные последовательности распадаются на
, последовательность имеет некоторую
периодическую структуру. Различные последовательности распадаются на ![]() статистически равнозначных классов, отличающихся лишь сдвигом начала (то есть
тем, какая именно буква называется первой). Сдвигом от 0 до
статистически равнозначных классов, отличающихся лишь сдвигом начала (то есть
тем, какая именно буква называется первой). Сдвигом от 0 до ![]() любая из этих последовательностей может быть сделана статистически эквивалентной
любой другой. Простым примером с
любая из этих последовательностей может быть сделана статистически эквивалентной
любой другой. Простым примером с ![]() может служить случай с
тремя буквами
может служить случай с
тремя буквами ![]() . За буквой
. За буквой ![]() следует либо
следует либо ![]() , либо
, либо ![]() с вероятностями
с вероятностями ![]() и
и ![]() соответственно.
За буквами же
соответственно.
За буквами же ![]() или
или ![]() всегда следует
всегда следует ![]() .
Тогда типичной последовательностью будет
.
Тогда типичной последовательностью будет
a b a c a c a c a b a c a b a b a c a c.
Данный случай не очень важен для нашей работы.
Если же нарушается первое условие, граф распадается на несколько подграфов,
на каждом из которых это условие выполнено. Мы будем предполагать, что на
каждом из них выполнено также и второе условие. В это случае мы имеем
``смешанный'' источник, состоящий из нескольких чистых, соответствующих
каждому из субграфов. Если ![]() ,
, ![]() ,
, ![]() -
чистые компоненты, можно записать
-
чистые компоненты, можно записать
где ![]() - вероятность компонента источника
- вероятность компонента источника ![]() .
.
Физически ситуация представляет из себя следующее. Есть несколько различных
источников ![]() ,
, ![]() ,
, ![]() , каждый
из которых статистически однороден (т.е. эргодичен). Мы не можем сказать
a priori, который из них будет использован, но если
последовательность начинается в каком-то из чистых компонентов, в дальнейшем
она в нем и останется, бесконечно продолжаясь в соответствии с его статистической
структурой.
, каждый
из которых статистически однороден (т.е. эргодичен). Мы не можем сказать
a priori, который из них будет использован, но если
последовательность начинается в каком-то из чистых компонентов, в дальнейшем
она в нем и останется, бесконечно продолжаясь в соответствии с его статистической
структурой.
Для примера возьмем два из вышеприведенных процессов и примем ![]() и
и ![]() .
Последовательность от смешанного источника
.
Последовательность от смешанного источника
может быть получена выбором ![]() либо
либо ![]() с вероятностями
0.2 и 0.8 и генерированием последовательности в соответствием с этим выбором.
с вероятностями
0.2 и 0.8 и генерированием последовательности в соответствием с этим выбором.
В дальнейшем мы будет предполагать источник эргодическим, если специально не указано обратное. Это предположение позволяет отождествить средние по последовательности со средними по ансамблю всех возможных последовательностей (вероятность отличия равна нулю). К примеру, относительная частота буквы A в некоторой бесконечной последовательности с вероятностью единица будет равна относительной частоте ее в ансамбле последовательностей.
Если ![]() - вероятность состояния
- вероятность состояния ![]() и
и ![]() -
вероятность перехода в в состояние
-
вероятность перехода в в состояние ![]() , ясно, что для стационарности процесса
, ясно, что для стационарности процесса
![]() должна удовлетворять условию равновесия:
должна удовлетворять условию равновесия:
В эргодическом случае можно показать, что при любых начальных условиях
вероятности ![]() оказаться в состоянии
оказаться в состоянии ![]() после
после
![]() символов стремятся к равновесному значению при
символов стремятся к равновесному значению при ![]() .
.
Мы представили дискретный источник информации марковским процессом. Можем ли мы определить некоторую величину, характеризующую в некотором смысле количество информации, ``производимой'' таким процессом, или, точнее, темп ``производства'' информации?
Пусть у нас есть набор возможных событий с вероятностями ![]() .
Эти вероятности известны и больше про эти события ничего не известно.
Можно ли найти меру совершаемого ``выбора'' одного из событий или же
неопределенности получаемого результата?
.
Эти вероятности известны и больше про эти события ничего не известно.
Можно ли найти меру совершаемого ``выбора'' одного из событий или же
неопределенности получаемого результата?
Разумно потребовать от такой меры, скажем, ![]() , следующих свойств:
, следующих свойств:
При разбиении одного из возможных выборов на два, исходная величина ![]() должна быть взвешенной суммой отдельных величин
должна быть взвешенной суммой отдельных величин ![]() . Смысл этого
иллюстрируется на рис. 6.
. Смысл этого
иллюстрируется на рис. 6.
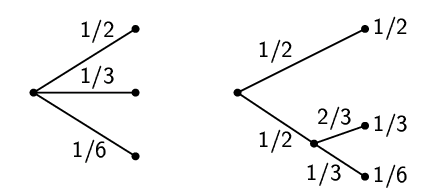
Слева мы имеем три возможности ![]() ,
, ![]() ,
, ![]() . Справа, мы сначала выбираем
между двумя возможностями вероятностью
. Справа, мы сначала выбираем
между двумя возможностями вероятностью ![]() каждая, и, в случае
выбора второй, делаем следующий выбор с вероятностями
каждая, и, в случае
выбора второй, делаем следующий выбор с вероятностями ![]() ,
,
![]() . Конечные результаты имеют те же вероятности, что
и раньше. В данном конкретном случае требование сводится к
. Конечные результаты имеют те же вероятности, что
и раньше. В данном конкретном случае требование сводится к
Коэффициент ![]() возникает из-за того, что второй выбор
делается лишь в половине случаев.
возникает из-за того, что второй выбор
делается лишь в половине случаев.
В приложении 2 доказывается следующий результат:
Теорема 2: Единственная $H$, удовлетворяющая трем вышеприведенным условиям, имеет вид:
где ![]() - некоторая положительная константа.
- некоторая положительная константа.
Эта теорема, как и предположения, требуемые для ее доказательства, никак не будут использоваться в дальнейшем. Они приведены главным образом для придания некоторой правдоподобности нашим последующим определениям. Их истинным доказательством, однако, послужат их приложения.
Величины вида ![]() (константа
(константа ![]() отвечает за выбор системы единиц) играют центральную роль в теории информации
как меры информации, выбора и неопределенности. Такой же вид имеет выражение
для энтропии в некоторых формулировках статистической механики (см., к примеру,
R. C. Tolman, Principles of Statistical Mechanics,
Oxford, Clarendon, 1938.), где
отвечает за выбор системы единиц) играют центральную роль в теории информации
как меры информации, выбора и неопределенности. Такой же вид имеет выражение
для энтропии в некоторых формулировках статистической механики (см., к примеру,
R. C. Tolman, Principles of Statistical Mechanics,
Oxford, Clarendon, 1938.), где ![]() - вероятность найти
систему в ячейке
- вероятность найти
систему в ячейке ![]() ее фазового пространства.
ее фазового пространства. ![]() тогда,
к примеру, совпадает с
тогда,
к примеру, совпадает с ![]() в знаменитой теореме Больцмана.
Назовем
в знаменитой теореме Больцмана.
Назовем ![]() энтропией набора вероятностей
энтропией набора вероятностей ![]() .
Будем обозначать
.
Будем обозначать ![]() энтропию случайной величины
энтропию случайной величины ![]() ;
здесь
;
здесь ![]() - не аргумент функции, а метка, призванная отличать
обозначение энтропии величины
- не аргумент функции, а метка, призванная отличать
обозначение энтропии величины ![]() от энтропии
от энтропии ![]() случайной величины
случайной величины ![]() .
.
Энтропия для случая двух возможностей с вероятностями ![]() и
и
![]() ,
,
изображена на рис. 7 как функция ![]() .
.
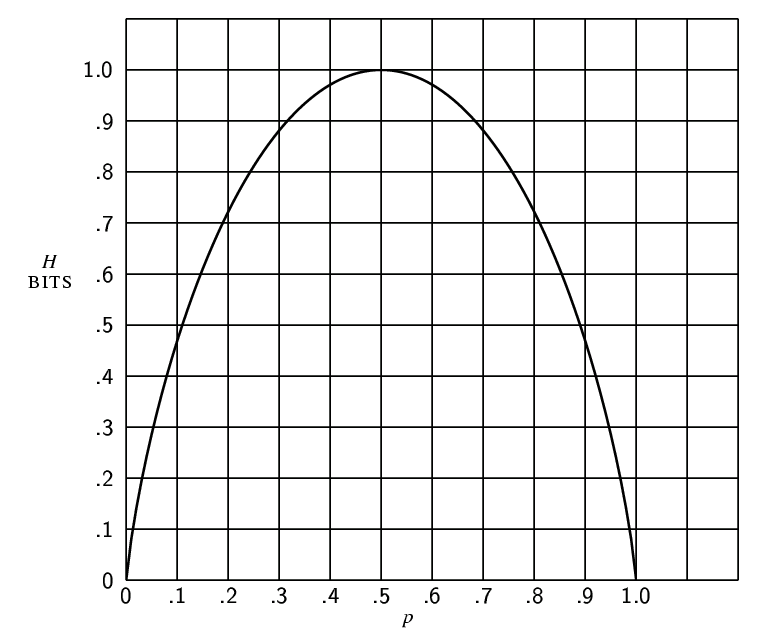
Величина ![]() обладает несколькими интересными свойствами,
делающими ее приемлемой мерой выбора или информации:
обладает несколькими интересными свойствами,
делающими ее приемлемой мерой выбора или информации:
1. ![]() тогда и только тогда, когда все
тогда и только тогда, когда все ![]() за исключением одного равны нулю, а один - единице, то есть величина
за исключением одного равны нулю, а один - единице, то есть величина
![]() обращается в ноль лишь тогда, когда мы уверены в выборе.
Во всех остальных случаях
обращается в ноль лишь тогда, когда мы уверены в выборе.
Во всех остальных случаях ![]() положительна.
положительна.
2. Для данного ![]()
![]() принимает максимальное значение
тогда, когда все $p_i$ равны между собой (и, соответственно,
равны
принимает максимальное значение
тогда, когда все $p_i$ равны между собой (и, соответственно,
равны ![]() ). Интуитивно понятно, что это - наиболее неопределенная
ситуация.
). Интуитивно понятно, что это - наиболее неопределенная
ситуация.
3. Рассмотрим два события, ![]() и
и ![]() , причем
первому соответствует
, причем
первому соответствует ![]() возможностей, а второму -
возможностей, а второму - ![]() .
Пусть
.
Пусть ![]() - вероятность совместного появления
- вероятность совместного появления ![]() для
первого и
для
первого и ![]() для второго. Энтропия такого совместного события равна
для второго. Энтропия такого совместного события равна
в то время как
Легко показать, что
причем равенство достигается лишь при независимости событий (т.е. при ![]() ). Неопределенность совместного события меньше или равна сумме
неопределенностей событий по-отдельности.
). Неопределенность совместного события меньше или равна сумме
неопределенностей событий по-отдельности.
4. Любое изменение, направленное на уравнивание вероятностей ![]() , увеличивает
, увеличивает ![]() . Так, если
. Так, если ![]() и мы
увеличиваем
и мы
увеличиваем ![]() , уменьшая
, уменьшая ![]() на ту же величину,
так что
на ту же величину,
так что ![]() и
и ![]() оказываются ближе бруг к другу,
величина
оказываются ближе бруг к другу,
величина ![]() возрастает. В более общем случае, если мы производим
некоторую процедуру ``усреднения''
возрастает. В более общем случае, если мы производим
некоторую процедуру ``усреднения'' ![]() вида
вида
где ![]() и все
и все ![]() ,
величина
,
величина ![]() возрастает (за исключением специального случая, при котором
значения
возрастает (за исключением специального случая, при котором
значения ![]() просто меняются местами; в этом случае $H$, естественно, остается
неизменной).
просто меняются местами; в этом случае $H$, естественно, остается
неизменной).
5.Рассмотрим два случайных события, ![]() и
и ![]() , как в
пункте 3, не обязательно независимых. Для любого значения
, как в
пункте 3, не обязательно независимых. Для любого значения ![]() , которое
может принимать
, которое
может принимать ![]() , существует условная вероятность
, существует условная вероятность ![]() того, что
того, что ![]() примет значение
примет значение ![]() . Она имеет вид
. Она имеет вид
Определим условную энтропию величины ![]() ,
, ![]() ,
как среднюю энтропию
,
как среднюю энтропию ![]() при каждом значении
при каждом значении ![]() , взвешенную
в соответствии с вероятностью получения данного значения
, взвешенную
в соответствии с вероятностью получения данного значения ![]() . Она равна
. Она равна
Это величина показывает, насколько в среднем является неопределенной ![]() ,
если мы знаем
,
если мы знаем ![]() . Подставляя
. Подставляя ![]() , получаем
, получаем
или
Неопределенность (или энтропия) совместного события ![]() равна
сумме неопределенности
равна
сумме неопределенности ![]() и неопределенности
и неопределенности ![]() при
известной величине
при
известной величине ![]() .
.
6. Из пунктов 3 и 5 имеем
Таким образом,
Неопределенность ![]() никогда не увеличивается при конкретизации
никогда не увеличивается при конкретизации ![]() .
Она уменьшается, если только
.
Она уменьшается, если только ![]() и
и ![]() не являются независимыми
событиями. В последнем же случае она остается неизменной.
не являются независимыми
событиями. В последнем же случае она остается неизменной.
Рассмотрим дискретный источник информации описанного выше типа. Для каждого
из состояний ![]() существует набор вероятностей
существует набор вероятностей ![]() генерации различных возможных символов
генерации различных возможных символов ![]() , что соответствует
энторпии данного состояния
, что соответствует
энторпии данного состояния ![]() . Определим энтропию источника
как среднее всех
. Определим энтропию источника
как среднее всех ![]() , взвешенных согласно вероятностям
соответствующих состояний:
, взвешенных согласно вероятностям
соответствующих состояний:
Это энтропия в расчете на символ текста. Если марковский процесс имеет определенный темп, можно также определить энтрпоию в секунду
шде ![]() - средняя частота (реализаций в секунду) состояния
- средняя частота (реализаций в секунду) состояния
![]() . Ясно, что
. Ясно, что
где ![]() - среднее число символов, генерируемых за секунду.
- среднее число символов, генерируемых за секунду.
![]() или
или ![]() характеризуют количество информации,
производимой источником в расчете на символ или на секунду. Если за основание
логарифма принята двойка, они представляют собой биты на символ или биты в секунду.
характеризуют количество информации,
производимой источником в расчете на символ или на секунду. Если за основание
логарифма принята двойка, они представляют собой биты на символ или биты в секунду.
Если последовательные символы независимы, то ![]() есть просто
есть просто ![]() , где
, где ![]() - вероятность символа
- вероятность символа ![]() .
Пусть мы имеем достаточно длинное сообщение, содержащее
.
Пусть мы имеем достаточно длинное сообщение, содержащее ![]() символов.
С высокой вероятностью в нем будет примерно
символов.
С высокой вероятностью в нем будет примерно ![]() вхождений первого
символа,
вхождений первого
символа, ![]() - второго, и так далее. Таким образом вероятность
данного собщения будет примерно равна
- второго, и так далее. Таким образом вероятность
данного собщения будет примерно равна
или же
![]() , таким образом, есть логарифм обратной вероятности типичной
длинной последовательности, деленный на число символов в ней. Аналогичный
результат имеет место для произвольного источника. Более точно, можно
сформулиовать (см. приложение 3)
, таким образом, есть логарифм обратной вероятности типичной
длинной последовательности, деленный на число символов в ней. Аналогичный
результат имеет место для произвольного источника. Более точно, можно
сформулиовать (см. приложение 3)
Теорема 3: Для произвольных ![]() и
и ![]() можно найти такое
можно найти такое ![]() , что последовательности произвольной длины
, что последовательности произвольной длины
![]() распадаются на два класса:
распадаются на два класса:
![]() .
.
Иными словами, практически наверняка достаточно
близко к ![]() при достаточно больших
при достаточно больших ![]() .
.
Похожий результат имеет место для числа последовательностей с различными
вероятностями. Рассмотрим вновь последовательности длины ![]() и
отсортируем их по убыванию вероятности. Определим
и
отсортируем их по убыванию вероятности. Определим ![]() как число
послдовательностей, которые мы должны выбрать из данного набора, начиная с наиболее
вероятной, для получения суммарной вероятности
как число
послдовательностей, которые мы должны выбрать из данного набора, начиная с наиболее
вероятной, для получения суммарной вероятности ![]() .
.
Теорема 4:
при ![]() , не равных
, не равных ![]() или
или ![]() .
.
![]() может быть истолковано как число бит, требуемых для
выделения последовательности, если мы рассматриваем лишь наиболее вероятные
из них суммарной вероятностью
может быть истолковано как число бит, требуемых для
выделения последовательности, если мы рассматриваем лишь наиболее вероятные
из них суммарной вероятностью ![]() . Тогда -
число бин на символ для такого выделения. Теорема гласит, что для больших
. Тогда -
число бин на символ для такого выделения. Теорема гласит, что для больших
![]() оно не зависит от
оно не зависит от ![]() и равно
и равно ![]() . Темп
роста логарифма числа достаточно вероятных последовательностей дается
. Темп
роста логарифма числа достаточно вероятных последовательностей дается ![]() вне зависимости от того, как именно мы определяем эту ``достаточную вероятность''.
Благодаря этим результатам (доказываемым в приложении 3) для большинства задач
можно считать, что (достаточно длинных) последовательностей всего
вне зависимости от того, как именно мы определяем эту ``достаточную вероятность''.
Благодаря этим результатам (доказываемым в приложении 3) для большинства задач
можно считать, что (достаточно длинных) последовательностей всего ![]() ,
и каждая из них имеет вероятность
,
и каждая из них имеет вероятность ![]() .
.
Две следующих теоремы показывают, что ![]() и
и ![]() могут
быть определены посредством пределных переходов прямо из статистики сообщения,
без конкретизации различных состояний и вероятностей перехода.
могут
быть определены посредством пределных переходов прямо из статистики сообщения,
без конкретизации различных состояний и вероятностей перехода.
Теорема 5:
Пусть ![]() - вероятность последовательности символов
- вероятность последовательности символов ![]() от источника, и пусть
от источника, и пусть
где суммирование производится по всем последовательностям ![]() , содержащим
, содержащим
![]() символов. Тогда
символов. Тогда ![]() - монотонно убывающая функция
- монотонно убывающая функция
![]() и
и
Теорема 6:
Пусть ![]() - вероятность того, что за последовательностью
- вероятность того, что за последовательностью
![]() следует символ
следует символ ![]() , и
, и ![]() -
условная вероятность
-
условная вероятность ![]() после
после ![]() . Пусть
. Пусть
где суммирование производится по всем блокам ![]() длиной
длиной ![]() символов
и по всем символам
символов
и по всем символам ![]() . Тогда
. Тогда ![]() - монотонно убывающая
функция
- монотонно убывающая
функция ![]() ,
,
и ![]() .
.
Эти результаты получаются в приложении 3. Они показывают, что серия приближений
к ![]() может быть получена при рассмотрении статистической структуры
последовательностей длиной
может быть получена при рассмотрении статистической структуры
последовательностей длиной ![]() символов.
символов. ![]() является наилучшим приближением. Фактически
является наилучшим приближением. Фактически ![]() является энтропией
является энтропией
![]() -того приближения для источника, описанного выше типа. Если
статистическое влияние на расстояниях, больших
-того приближения для источника, описанного выше типа. Если
статистическое влияние на расстояниях, больших ![]() , отсутствует,
то есть если условная вероятность последуующего символа при знании
, отсутствует,
то есть если условная вероятность последуующего символа при знании ![]() предыдущего не изменяется конкретизацией любого предшествующего им, то
предыдущего не изменяется конкретизацией любого предшествующего им, то ![]() .
.
![]() , естественно, явлется условной энтропией последующего симвода при
знании
, естественно, явлется условной энтропией последующего симвода при
знании ![]() предыдущих, тогда как $G_N$ - энтропия на символ
блоков длины $N$.
предыдущих, тогда как $G_N$ - энтропия на символ
блоков длины $N$.
Назовем отношение энтропии источника к максимальному значению, которое она
может принимать, будучи ограниченной теми же предшествующими символами,
относительной энтропией. Это - наибольший возможный коэффициент сжатия
при кодировании с использованием того же самого алфавита. Назовем разность единицы
и относительной энтропии избыточностью. Избыточность английского языка,
при рассмотрении статистических структур на масштабах не более восьми букв,
составляет порядка ![]() . Это значит, что: когда мы пишем английский текст,
половина его определяется статистической структурой языка, а половина выбирается
нами свободно. Оценка
. Это значит, что: когда мы пишем английский текст,
половина его определяется статистической структурой языка, а половина выбирается
нами свободно. Оценка ![]() получается несколькими независимыми
методами, дающими примерно одинаковый результат, - расчетом энтропии приближений
к английскому языку, удалением с последующим восстановлением части букв из
английского текста, и так далее. Так, если текст может быть полностью восстановлен
после удаления из него половины букв, его избыточность должна быть больше
получается несколькими независимыми
методами, дающими примерно одинаковый результат, - расчетом энтропии приближений
к английскому языку, удалением с последующим восстановлением части букв из
английского текста, и так далее. Так, если текст может быть полностью восстановлен
после удаления из него половины букв, его избыточность должна быть больше ![]() .
Еще один метод основан на некторвых известных результатах криптографии.
.
Еще один метод основан на некторвых известных результатах криптографии.
Две крайности избыточности английской прозы - Основной Английский (Бейсик Инглиш, Basic English) и книга Джеймса Джойса ``Поминки по Финнегану''. Словарь Бейсик Инглиш ограничен 850 словами, и его избыточность очень велика, что отражается в уведичении обьема сообщения при переаоде его в данный диалект. Джойс же, наоборот, расширяет лексикон, достигая таким образом уплотнения семантического содержания.
С избыточностью языка связано существование загадок-кроссвордов. При нулевой
избыточности любое буквосочетание является приемлемым текстом, и любой двумерный
массив букв образует кроссворд. Если же избыточность достаточно велика, язык
налашаем слишком много ограничений, что делает невозможным существование больших
кроссвордов. Более тщательный анализ показывает, что при случайной
природе ограничений языка большие кроссворды возможны лишь при избыточности
его порядка ![]() . При избыточности
. При избыточности ![]() становятся
возможными трехмерные кроссворды, и так далее.
становятся
возможными трехмерные кроссворды, и так далее.
Мы все еще не представили математически операции, производимые передатчиком
и премником при кодировании и декодировании информации. Назовем оба этих
прибора ![]() . Преобразователь получает на вход
некоторый набор входных символов, и выдает набор выходных символов. Преобразователь
может иметь внутреннюю память, так что информация на выходе будет зависеть не только
от текущего поступившего на вход символа, но также и от всех предшествующих.
Мы будет считать внутреннюю память конечной, то есть предполагать наличие у преобразователя
конечного числа внутренних состояний
. Преобразователь получает на вход
некоторый набор входных символов, и выдает набор выходных символов. Преобразователь
может иметь внутреннюю память, так что информация на выходе будет зависеть не только
от текущего поступившего на вход символа, но также и от всех предшествующих.
Мы будет считать внутреннюю память конечной, то есть предполагать наличие у преобразователя
конечного числа внутренних состояний ![]() , таких, что символ на выходе
является функцией символа на входе и текущего состояния. Следующее состояние
является еще одной функцией этих двух величин. Таким образом, преобразователь
может быть описан двумя функциями:
, таких, что символ на выходе
является функцией символа на входе и текущего состояния. Следующее состояние
является еще одной функцией этих двух величин. Таким образом, преобразователь
может быть описан двумя функциями:
где
| - | | |
| - | состояние преобразователя при получении
| |
| - | выходной символ (или последовательность символов),
формируемый при получении символа |
Если выходной символ одного из преобразователей может быть подан на вход другого, их можно соединить последовательно и получить еще один преобразователь. Если существует преобразователь, преобразующий выходную информацию первого в его же входную, первый преобразователь назовем несингулярным, а второй - обратным к нему.
Теорема 7: Выходная последовательность преобразователя с конечным числом состояний является последовательностью от статистического источника с конечным числом состояний, с энтропией (в единицу времени), не большей энтропии входной последовательности. Если преобразователь является несингулярным, эти энтропии равны.
пусть ![]() описывает состояние источника, выдающего последовательность
символов
описывает состояние источника, выдающего последовательность
символов ![]() ,
, ![]() - состояние преобразователя,
дающего на выходе блоки символов
- состояние преобразователя,
дающего на выходе блоки символов ![]() . Систему можно описать
прямым произведением пространств их состояний, то есть пространством
пар
. Систему можно описать
прямым произведением пространств их состояний, то есть пространством
пар ![]() . Соединим две точки этого пространства
. Соединим две точки этого пространства
![]() и
и ![]() линией, если
линией, если
![]() может сгенерировать
может сгенерировать ![]() , переводящий
, переводящий
![]() в
в ![]() так, что эта линия дает вероятность
такого
так, что эта линия дает вероятность
такого ![]() . Пометим такую линию набором символов
. Пометим такую линию набором символов ![]() ,
выданных преобразователем. Энтропия его может быть рассчитана как взвешенная сумма
по всем состояниям. Если мы вначале просуммируем по
,
выданных преобразователем. Энтропия его может быть рассчитана как взвешенная сумма
по всем состояниям. Если мы вначале просуммируем по ![]() , результирующий
член будет не большим соответствующего для
, результирующий
член будет не большим соответствующего для ![]() , так как
энтропия не возрастает. Если преобразователь несингулярен, соединим его
со входом обратного ему. Если
, так как
энтропия не возрастает. Если преобразователь несингулярен, соединим его
со входом обратного ему. Если ![]() ,
, ![]() и
и ![]() -
энтропии на выходе источника, первого и второго преобразователей соответственно,
то
-
энтропии на выходе источника, первого и второго преобразователей соответственно,
то ![]() и, следовательно,
и, следовательно, ![]() .
.
Пусть мы имеем набор ограничений на возможные последовательности, которые
можно предстваить в виде линейного графа, подобного изображенному на рис. 2.
Если вероятности ![]() приписаны всевозможным линиям,
соединяющим состояние
приписаны всевозможным линиям,
соединяющим состояние ![]() с состоянием
с состоянием ![]() , эта система
становится источником. Одно из сопоставлений максимизирует энтропию на выходе
(см. приложение 4).
, эта система
становится источником. Одно из сопоставлений максимизирует энтропию на выходе
(см. приложение 4).
Теорема 8:
Пусть система ограничений рассматривается как канал с пропускной способностью
![]() . Если мы примем
. Если мы примем
где ![]() - длительность
- длительность ![]() -того символа,
переводящего систему из состояния
-того символа,
переводящего систему из состояния ![]() в
в ![]() , и
, и ![]() удовлетворяет условию
удовлетворяет условию
то $H$ максимальна и равна $C$.
Надлеащим выбором вероятностей перехода энтропия символов в канале может быть доведена до пропускной способности канала.
Теперь мы обоснуем интерпретацию ![]() как темпа генерации информации,
показав, что
как темпа генерации информации,
показав, что ![]() определяет требуемую для наиболее эффективного
кодирования пропускную способность канала.
определяет требуемую для наиболее эффективного
кодирования пропускную способность канала.
Теорема 9:
Пусть энтропия источника есть ![]() (бит на символ), а пропускная
способность канала -
(бит на символ), а пропускная
способность канала - ![]() (бит в секунду). Тогда возможно так
закодировать информацию от источника, что средний темп ее передачи по каналу будет
, где
(бит в секунду). Тогда возможно так
закодировать информацию от источника, что средний темп ее передачи по каналу будет
, где ![]() может быть сделана
в произвольной степени малой. Невозможно передать информацию в темпе, большем
.
может быть сделана
в произвольной степени малой. Невозможно передать информацию в темпе, большем
.
Утверждение теоремы о невозможносит передачи с темпом, большим ,
может быть доказана с использованием того, что энтропия подаваемого в канал
за секунду набора символов равна энтропии источника, так как преобразователь должен
быть несингулярным, и, кроме того, эта энтропия не может быть больше пропускной
способности канала. Следовательно, ![]() , и число символов
в секунду
, и число символов
в секунду ![]() .
.
Первая же часть теоремы доказывается двумя различными методами. Первый заключается
в рассмотрении набора всех последовательностей ![]() символов, генерируемых
источником. Для больших
символов, генерируемых
источником. Для больших ![]() мы можем разбить их на две группы:
содержащую последовательности короче
мы можем разбить их на две группы:
содержащую последовательности короче ![]() символов и
содержащую последовательности короче
символов и
содержащую последовательности короче ![]() (
(![]() здесь есть логарифм числа различных символов)
с полной вероятностью меньше
здесь есть логарифм числа различных символов)
с полной вероятностью меньше ![]() . С ростом
. С ростом ![]()
![]() и
и ![]() стремятся к нулю. Число сигналов длительности
стремятся к нулю. Число сигналов длительности ![]() в канале
больше
в канале
больше ![]() (где
(где ![]() мало) при
достаточно больших
мало) при
достаточно больших ![]() . Если мы примем
. Если мы примем
то число последовательностей символов канала для группы большой вероятности
будет бостаточно большим при больших ![]() и
и ![]() (и малой
(и малой ![]() ),
а кроме того, будет еще несколько последовательностей малой вероятности.
Группа высокой вероятности кодируется произвольным однозначным сопоставлением
с элементами этого множества. Остальные последовательности кодируются более
длинными последовательностями, начинающимися и заканчивающимися элементами,
не используемыми для кодирования группы высокой вероятности. Эти элементы
(отдельные символы или их группы) сигнализируют начало и конец для другой
кодировки. Между ними дается достаточное время для передачи сообщений
малой вероятности. Это требует
),
а кроме того, будет еще несколько последовательностей малой вероятности.
Группа высокой вероятности кодируется произвольным однозначным сопоставлением
с элементами этого множества. Остальные последовательности кодируются более
длинными последовательностями, начинающимися и заканчивающимися элементами,
не используемыми для кодирования группы высокой вероятности. Эти элементы
(отдельные символы или их группы) сигнализируют начало и конец для другой
кодировки. Между ними дается достаточное время для передачи сообщений
малой вероятности. Это требует
где ![]() мало. Средний темп передачи символов сообщения в секунду
тогда будет больше, чем
мало. Средний темп передачи символов сообщения в секунду
тогда будет больше, чем
С ростом ![]()
![]() ,
, ![]() и
и ![]() стремятся к нулю, а темп стремится к C / H.
стремятся к нулю, а темп стремится к C / H.
Другим способом такого кодирования (и. следовательно, доказательства теоремы)
можно описать следующим образом. Отсортируем сообщения длины ![]() по убыванию вероятности,
по убыванию вероятности, ![]() .
Пусть - суммарная вероятность вплоть до
.
Пусть - суммарная вероятность вплоть до
![]() (не включая
(не включая ![]() ). Вначале закодируем в двоичную
систему. Двоичным кодом для сообщения
). Вначале закодируем в двоичную
систему. Двоичным кодом для сообщения ![]() будет представление
будет представление
![]() двоичным числом. Это представление размещается на
двоичным числом. Это представление размещается на ![]() позициях, где
позициях, где ![]() - целое число, удовлетворяющее условию
- целое число, удовлетворяющее условию
Таким образом, сообщения с высокой вероятностью представляются более коротким кодом, чем маловероятные. Из этих неравенств получаем
Код для ![]() будет отличаться от всех последующих в одном или
более из составляющих его
будет отличаться от всех последующих в одном или
более из составляющих его ![]() символов, так как все остальные
символов, так как все остальные
![]() как минимум на
как минимум на ![]() больше, и их
двоичные представления различаются в первых
больше, и их
двоичные представления различаются в первых ![]() позициях.
Следовательно, все коды различны, и восстановление сообщения по его коду
возможно. Если последовательности канала сами по себе не являются двоичными,
они могут быть сведены к ним произвольным образом так, чтобы двоичный код
однозначно преобразовывался бы в сигнал, приемлемый для канала.
позициях.
Следовательно, все коды различны, и восстановление сообщения по его коду
возможно. Если последовательности канала сами по себе не являются двоичными,
они могут быть сведены к ним произвольным образом так, чтобы двоичный код
однозначно преобразовывался бы в сигнал, приемлемый для канала.
Среднее число ![]() двоичных цифр на символ исходного сообщения
может быть легко оценено. Имеем
двоичных цифр на символ исходного сообщения
может быть легко оценено. Имеем
В то же время
и следовательно
С ростом ![]()
![]() стремится к
стремится к ![]() , энтропии
источника, и
, энтропии
источника, и ![]() стремится к
стремится к ![]() .
.
Осюда видно, что неэффективность кодирования, то есть использование не всех из ![]() символов, может быть доведена до
символов, может быть доведена до ![]() с добавлением разницы
между истинной энтропией
с добавлением разницы
между истинной энтропией ![]() и ее оценкой
и ее оценкой ![]() по
последовательностям длины
по
последовательностям длины ![]() . Процент времени, избыточного
по отношению к идеальному случаю, соответственно, может быть сделан меньшим
. Процент времени, избыточного
по отношению к идеальному случаю, соответственно, может быть сделан меньшим
Этот метод кодирования практически совпадает с предложенным независимо
R. M. Fano (Technical Report No. 65, The Research Laboratory of Electronics, M.I.T., March 17, 1949.),
который заключается в сортировке сообщений длины ![]() по убыванию их вероятности.
В дальнейшем эти сообщения делятся на две группы с как можно более близкими
полными вероятностями. Для сообщений первой группы первой двоичной цифрой будет
0, для второй - 1. Группы таким же образом делятся далее, вплоть до того, что
в каждой группе остается по одному сообщению. Легко видеть, что с небольшой
разницей (в основном в последнем знаке) это аналогично процессу, описанному нами
выше.
по убыванию их вероятности.
В дальнейшем эти сообщения делятся на две группы с как можно более близкими
полными вероятностями. Для сообщений первой группы первой двоичной цифрой будет
0, для второй - 1. Группы таким же образом делятся далее, вплоть до того, что
в каждой группе остается по одному сообщению. Легко видеть, что с небольшой
разницей (в основном в последнем знаке) это аналогично процессу, описанному нами
выше.
В электротехнике для получения максимальной передачи мощности от генератора
к нагрузке генератор должен обладать такими свойствами, чтобы с точки зрения
нагрузки его сопротивление было равно сопротивлению ее. В нашем случае ситуация примерно
аналогична. Преобразователь, который занимается кодированием сообщения, должен
соответствовать источнику в статистическом смысле. Источник и преобразователь
с точки зрения канала должны обладать статистическими свойствами источника,
максимизирующего энтропию в канале. Содержанием теоремы 9 является то, что,
хотя идеальное соответствие в общем случае невозможно, мы можем приближаться к нему
с какой угодно степенью точности. Отношение действительного темпа передачи
к пропускной способности канала ![]() может быть названо
эффективностью системы кодирования. Она, естественно, равна отношению
действительной энтропии символов в канале к максимально возможному значению.
может быть названо
эффективностью системы кодирования. Она, естественно, равна отношению
действительной энтропии символов в канале к максимально возможному значению.
В общем случае идеальное или почти идеальное кодирование требует длительных задержек и передатчике и приемнике. В рассматриваемом случае отсутствия шума главной функцией этих задержек является достаточно тщательное сопоставление вероятностей последовательностей соответствующих длин. При хорошем кодировании логарифм совместной вероятности длинного сообщения должен быть пропорционален длительности соответствующего сигнала, точнее
должно быть мало практически для всех длинных сообщений.
Если источник генерирует только одно фиксированное сообщение, его энтропия
равна нулю, и канал не требуется. К примеру, вычислительная машина для расчета
последовательных цифр числа ![]() выдает детерминированную
последовательность без случайной составляющей. Для передачи такого сигнала нет
нужды в канале - достаточно построить вторую аналогичную машину. Однако, иногда
это непрактично. В таком случае мы можем пренебречь некоторой информацией
о структуре сигнала. Можно рассматривать цифры числа
выдает детерминированную
последовательность без случайной составляющей. Для передачи такого сигнала нет
нужды в канале - достаточно построить вторую аналогичную машину. Однако, иногда
это непрактично. В таком случае мы можем пренебречь некоторой информацией
о структуре сигнала. Можно рассматривать цифры числа ![]() как
случайную последовательность и разработать систему для передачи произвольной
цифровой информации. Аналогично мы могли бы воспользоваться лишь частью нашего
знания статистической структуры английского языка. Для такого случая можно рассмотреть
источник с максимальной энтропией, удовлетворяющий выбранным нами статистическим
условиям. Энтропия такого источника определяет пропускную способность канала,
которая является необходимой и достаточной. Так, в случае передачи числа
как
случайную последовательность и разработать систему для передачи произвольной
цифровой информации. Аналогично мы могли бы воспользоваться лишь частью нашего
знания статистической структуры английского языка. Для такого случая можно рассмотреть
источник с максимальной энтропией, удовлетворяющий выбранным нами статистическим
условиям. Энтропия такого источника определяет пропускную способность канала,
которая является необходимой и достаточной. Так, в случае передачи числа ![]() единственным статистическим условием является то, что все символы выбираются из
набора
единственным статистическим условием является то, что все символы выбираются из
набора ![]() ; для английского текста мы можем оставить
лишь требование соответствия частот букв. Тогда источник с максимальной
энтропией является первым приближением к английскому языку, и его энтропия
определяет требуемую пропускную способность канала.
; для английского текста мы можем оставить
лишь требование соответствия частот букв. Тогда источник с максимальной
энтропией является первым приближением к английскому языку, и его энтропия
определяет требуемую пропускную способность канала.
В качестве простого примера вышеизложенных результатов рассмотрим источник,
генерирующий последовательность независимых букв, выбранных из A, B, C, D
с вероятностями ![]() ,
, ![]() ,
, ![]() ,
, ![]() соответственно. Тогда
соответственно. Тогда
Следовательно, для такого источника можно разработать систему представления
сообщений двоичным кодом со степенью сжатия вплоть до ![]() двоичных
цифр на символ. В данном примере это предельное значение может быть достигнуто
при использовании следующего кода (полученного методом, использованным во
втором варианте доказательства теоремы 9):
двоичных
цифр на символ. В данном примере это предельное значение может быть достигнуто
при использовании следующего кода (полученного методом, использованным во
втором варианте доказательства теоремы 9):
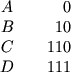
Среднее число двоичных знаков, использованных для кодирования последовательности
длиной ![]() символов будет
символов будет
Легко видеть, что двоичные знаки 0 и 1 имеют вероятности ![]() каждый,
следовательно,
каждый,
следовательно, ![]() для закодированной последовательности равно
одному биту на символ. Так как в среднем мы имеем
для закодированной последовательности равно
одному биту на символ. Так как в среднем мы имеем ![]() двоичных
знаков на исходный символ, энтропия в единицу времени остается неизменной.
Наибольшей возможной энтропией исходного набора будет
двоичных
знаков на исходный символ, энтропия в единицу времени остается неизменной.
Наибольшей возможной энтропией исходного набора будет ![]() ,
достигаемая при вероятностях букв
,
достигаемая при вероятностях букв ![]() ,
, ![]() ,
, ![]() ,
, ![]() , равных
$\frac14$ каждая. Таким образом, относительная энтропия равна
, равных
$\frac14$ каждая. Таким образом, относительная энтропия равна ![]() Двоичная последовательность может быть отображена на множество
исходных символов при помощи следующей таблицы:
Двоичная последовательность может быть отображена на множество
исходных символов при помощи следующей таблицы:

Такое двойное преобразование кодирует исходное сообщение теми же символами,
но с коэффициентом сжатия ![]() .
.
В качестве еще одного примера рассмотрим источник, выдающий буквы A и B
с вероятностями ![]() для A и
для A и ![]() для B.
При
для B.
При ![]()
В такой ситуации можно построить достаточно хорошую систему кодирования сообщений
в двоичном канале, посылая некоторую специльную последовательность, скажем,
0000, для маловероятного символа A, и затем число, характеризующее
количество следующих за ним символов B. Это количество может быть
охарактеризовано двоичным представлением при удалении всех чисел, содержащих
специальную последовательность. В нашем случае все числа вплоть до 16 представляются
как обычно, 16 представляется следующим числом, не содержащим специальной последовательности,
а именно ![]() , и так далее.
, и так далее.
Можно показать, что при ![]() система кодирования стремится к
идеальной при надлежащем выборе специальной последовательности.
система кодирования стремится к
идеальной при надлежащем выборе специальной последовательности.